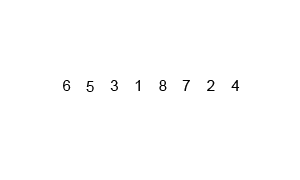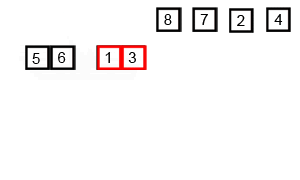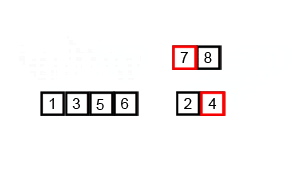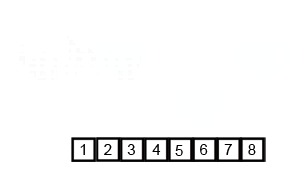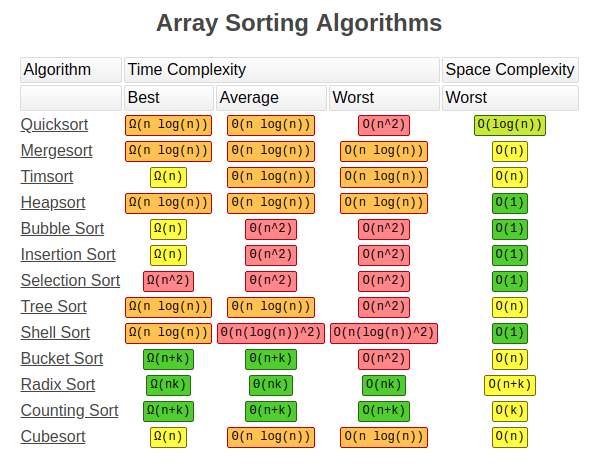
Sorting is a skill that every software engineer and developer needs some knowledge of. Not only to pass coding interviews but as a general understanding of programming itself. The different sorting algorithms are a perfect showcase of how algorithm design can have such a strong effect on program complexity, speed, and efficiency.

sorting algorithms complexity

Let’s take a tour of the top 6 sorting algorithms and see how we can implement them in Python!

Bubble Sort

Bubble sort is the one usually taught in introductory CS classes since it clearly demonstrates how sort works while being simple and easy to understand. Bubble sort steps through the list and compares adjacent pairs of elements. The elements are swapped if they are in the wrong order. The pass through the unsorted portion of the list is repeated until the list is sorted. Because Bubble sort repeatedly passes through the unsorted part of the list, it has a worst case complexity of O(n²).

Bubble Sort Algorithm

def bubble_sort(arr):
    def swap(i, j):
        arr[i], arr[j] = arr[j], arr[i]

    n = len(arr)
    swapped = True
    
    x = -1
    while swapped:
        swapped = False
        x = x + 1
        for i in range(1, n-x):
            if arr[i - 1] > arr[i]:
                swap(i - 1, i)
                swapped = True
                    
return arr

Performance

Bubble sort has a worst-case and average complexity of O (n²), where n is the number of items being sorted. Most practical sorting algorithms have substantially better worst-case or average complexity, often O(n log n). Even other О(n2) sorting algorithms, such as insertion sort , generally run faster than bubble sort, and are no more complex. Therefore, bubble sort is not a practical sorting algorithm.

The only significant advantage that bubble sort has over most other algorithms, even quicksort , but not insertion sort , is that the ability to detect that the list is sorted efficiently is built into the algorithm. When the list is already sorted (best-case), the complexity of bubble sort with a swap-checking variable is only O(n) (although the most basic implementation is O(n2) even in the best-case). By contrast, most other algorithms, even those with better average-case complexity , perform their entire sorting process on the set and thus are more complex. However, not only does insertion sort share this advantage, but it also performs better on a list that is substantially sorted (having a small number of inversions ).

Selection Sort

Selection sort is also quite simple but frequently outperforms bubble sort. If you are choosing between the two, it’s best to just default right to selection sort . With Selection sort , we divide our input list / array into two parts: the sublist of items already sorted and the sublist of items remaining to be sorted that make up the rest of the list. We first find the smallest element in the unsorted sublist and place it at the end of the sorted sublist. Thus, we are continuously grabbing the smallest unsorted element and placing it in sorted order in the sorted sublist. This process continues iteratively until the list is fully sorted.

Selection Sort Algorithm

def selection_sort(arr):        
    for i in range(len(arr)):
        minimum = i
        
        for j in range(i + 1, len(arr)):
            # Select the smallest value
            if arr[j] < arr[minimum]:
                minimum = j

        # Place it at the front of the 
        # sorted end of the array
        arr[minimum], arr[i] = arr[i], arr[minimum]
            
return arr

Performance

Selection sort is greatly outperformed on larger arrays by Θ(n log n) divide-and-conquer algorithms such as mergesort . However, insertion sort or selection sort are both typically faster for small arrays (i.e. fewer than 10–20 elements). A useful optimization in practice for the recursive algorithms is to switch to insertion sort or selection sort for "small enough" sublists.

Insertion sort

Insertion sort is a simple sorting algorithm that builds the final sorted array (or list) one item at a time. It is much less efficient on large lists than more advanced algorithms such as quicksort , heapsort , or merge sort . However, insertion sort provides several advantages:

• Simple implementation
• Efficient for (quite) small data sets, much like other quadratic sorting algorithms
• More efficient in practice than most other simple quadratic (i.e., O(n2)) algorithms such as selection sort or bubble sort
• Stable; i.e., does not change the relative order of elements with equal keys
• In-place; i.e., only requires a constant amount O(1) of additional memory space
• Online; i.e., can sort a list as it receives it

Insertion sort is both faster and well-arguably more simplistic than both bubble sort and selection sort. Funny enough, it’s how many people sort their cards when playing a card game! On each loop iteration, insertion sort removes one element from the array. It then finds the location where that element belongs within another sorted array and inserts it there. It repeats this process until no input elements remain.

Insertion Sort Algorithm

def insertion_sort(arr):
        
    for i in range(len(arr)):
        cursor = arr[i]
        pos = i
        
        while pos > 0 and arr[pos - 1] > cursor:
            # Swap the number down the list
            arr[pos] = arr[pos - 1]
            pos = pos - 1
        # Break and do the final swap
        arr[pos] = cursor

return arr

Merge Sort

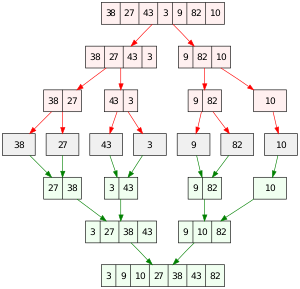
In computer science, merge sort (also commonly spelled mergesort) is an efficient, general-purpose, comparison-based sorting algorithm . Most implementations produce a stable sort , which means that the order of equal elements is the same in the input and output. Merge sort is a divide and conquer algorithm that was invented by John von Neumann in 1945.

Merge sort is a perfectly elegant example of a Divide and Conquer algorithm. It simple uses the 2 main steps of such an algorithm:

(1) Divide the unsorted list into n sublists, each containing one element (a list of one element is considered sorted).

(2) Repeatedly merge i.e conquer the sublists together 2 at a time to produce new sorted sublists until all elements have been fully merged into a single sorted array.

Merge Sort Algorithm

def merge_sort(arr):
    # The last array split
    if len(arr) <= 1:
        return arr
    mid = len(arr) // 2
    # Perform merge_sort recursively on both halves
    left, right = merge_sort(arr[:mid]), merge_sort(arr[mid:])

    # Merge each side together
    return merge(left, right, arr.copy())


def merge(left, right, merged):

    left_cursor, right_cursor = 0, 0
    while left_cursor < len(left) and right_cursor < len(right):
      
        # Sort each one and place into the result
        if left[left_cursor] <= right[right_cursor]:
            merged[left_cursor+right_cursor]=left[left_cursor]
            left_cursor += 1
        else:
            merged[left_cursor + right_cursor] = right[right_cursor]
            right_cursor += 1
            
    for left_cursor in range(left_cursor, len(left)):
        merged[left_cursor + right_cursor] = left[left_cursor]
        
    for right_cursor in range(right_cursor, len(right)):
        merged[left_cursor + right_cursor] = right[right_cursor]

return merged

A recursive merge sort algorithm used to sort an array of 7 integer values. These are the steps a human would take to emulate merge sort (top-down)

Quick Sort

Quicksort is a comparison sort , meaning that it can sort items of any type for which a "less-than" relation (formally, a total order ) is defined. It is still a commonly used algorithm for sorting. Quicksort can operate in-place on an array, requiring small additional amounts of memory to perform the sorting.

Quick sort is also a divide and conquer algorithm like merge sort . Although it’s a bit more complicated, in most standard implementations it performs significantly faster than merge sort and rarely reaches its worst case complexity of O(n²). It has 3 main steps:

1. We first select an element which we will call the pivot from the array.

2. Partitioning: reorder the array so that all elements with values less than the pivot come before the pivot, while all elements with values greater than the pivot come after it (equal values can go either way). After this partitioning, the pivot is in its final position. This is called the partition operation.

3. Recursively apply the above steps to the sub-array of elements with smaller values and separately to the sub-array of elements with greater values.

Quick Sort Algorithm

def partition(array, begin, end):
    pivot_idx = begin
    for i in xrange(begin+1, end+1):
        if array[i] <= array[begin]:
            pivot_idx += 1
            array[i], array[pivot_idx] = array[pivot_idx], array[i]
    array[pivot_idx], array[begin] = array[begin], array[pivot_idx]
    return pivot_idx

def quick_sort_recursion(array, begin, end):
    if begin >= end:
        return
    pivot_idx = partition(array, begin, end)
    quick_sort_recursion(array, begin, pivot_idx-1)
    quick_sort_recursion(array, pivot_idx+1, end)

def quick_sort(array, begin=0, end=None):
    if end is None:
        end = len(array) - 1
    
return quick_sort_recursion(array, begin, end)

Quick Sort Algorithm